Czemu rozkład Gaussa jest ,,normalny”? De Moivre, wzór Stirlinga i Laplace

Zamieszczono przez

Skąd się bierze wszechobecność rozkładu Gaussa? Jednym z powodów jest rozkład dwumianowy. Rozpatrzmy prościutki model. Przyjmijmy, że wzrost dorosłego mężczyzny warunkowany jest czterdziestoma genami w taki sposób, że każdy z nich może zwiększyć wzrost o 2 cm ponad pewne minimum albo nie zwiększyć. Zygota, z której powstaliśmy, wylosowała 40 genów i każdy z nich z prawdopodobieństwem p=\frac{1}{2} mógł dodać nam 2 cm wzrostu. Jeśli za minimum fizjologiczne uznamy 140 cm, to możliwy jest każdy wynik z przedziału (140, 220). Oczywiście, nie należy traktować tego przykładu dosłownie. Matematycznie oznaczałoby to 40 niezależnych losowań z prawdopodobieństwem sukcesu p. Rozkład liczby sukcesów wygląda wówczas następująco:

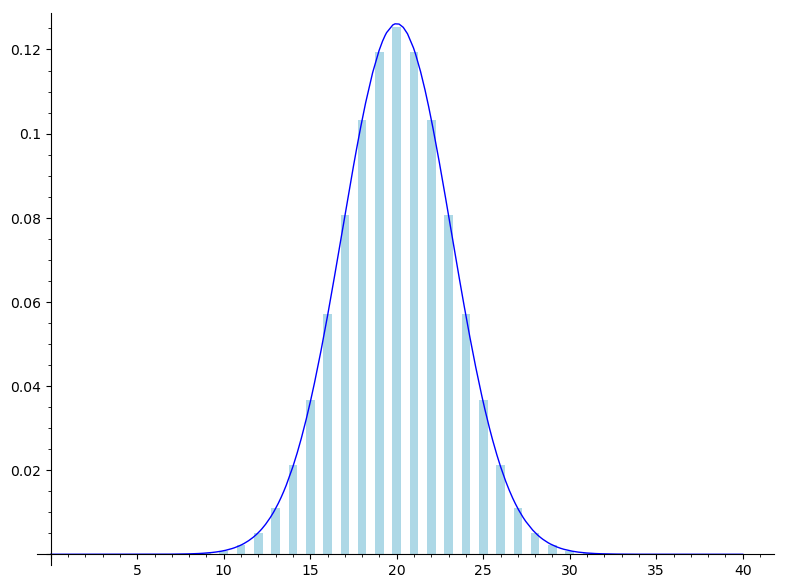
Dyskretny rozkład dwumianowy został tu przedstawiony z przybliżającym go rozkładem Gaussa. Naszym celem będzie zrozumienie, czemu takie przybliżenie działa, gdy mamy do czynienia z dużą liczbą prób.

Zacznijmy od samego rozkładu dwumianowego. Dla dwóch prób sytuacja wygląda tak (p – prawdopodobieństwo sukcesu, q=1-p – prawdopodobieństwo porażki):

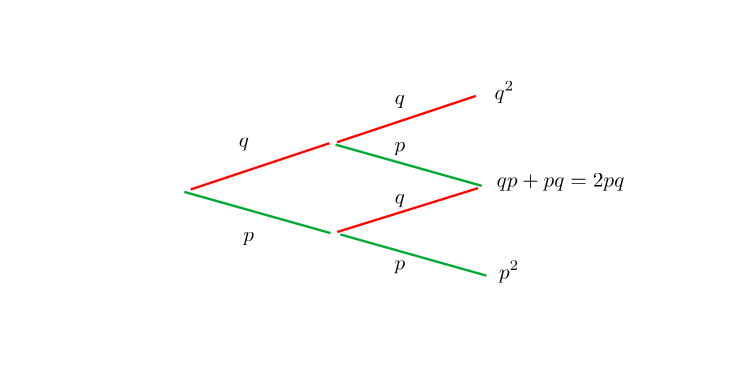
Każda droga z lewa na prawo oznacza konkretny wynik. Wzdłuż drogi prawdopodobieństwa się mnożą, ponieważ są to niezależne próby (definicja zdarzeń niezależnych). Zeru sukcesów odpowiada prawdopodobieństwo q^2, dwóm sukcesom p^2. Jeden sukces możemy osiągnąć na dwa sposoby: sukces-porażka albo porażka-sukces, prawdopodobieństwa należy dodać, jeśli interesuje nas wyłącznie całkowita liczba sukcesów, a nie jej konkretna realizacja. Łatwo zauważyć związek z dwumianem Newtona

(p+q)^n=(p+q)(p+q)\ldots (p+q),

gdzie mamy n czynników. Każdy wynik to wybór jednego z dwóch składników nawiasu: p albo q. Mnożymy je kolejno przez siebie, co odpowiada losowaniom, a następnie dodajemy. Oczywiście suma wszystkich prawdopodobieństw równa jest 1. Składniki zawierające k sukcesów mają czynnik p^k. Wzór Newtona (znany zresztą przed Newtonem) daje nam

(p+q)^n=\displaystyle \sum_{k=0}^{n}{n\choose k}p^k q^{n-k}.

Prawdopodobieństwo k sukcesów jest równe

P(k)=\displaystyle {n\choose k}p^k q^{n-k}.

Jest to nasz punkt wyjścia. Przy dużych wartościach n obliczanie symboli Newtona było w XVIII wieku trudne, ponieważ występują tam silnie dużych liczb. Zwłaszcza w rejonie środka rozkładu obliczenia takie były kłopotliwe, ponieważ zostaje wiele czynników, które się nie skracają. Abraham de Moivre, francuski protestant zmuszony do emigracji z ojczyzny z przyczyn religijnych, spędził życie w Londynie, ucząc matematyki. Podobno jeździł po Londynie od ucznia do ucznia z kolejnymi kartkami wyrwanymi z Matematycznych zasad Newtona i w wolnym czasie zgłębiał treść tej masywnej księgi. De Moivre podał sposób przybliżania P(k) oraz wartości silni – to drugie przybliżenie nazywamy dziś wzorem Stirlinga od nazwiska drugiego matematyka, który w tym czasie zajmował się tym zagadnieniem.

Zaczniemy od P(k). Jeśli spojrzeć na histogram z obrazka rzuca się w oczy ogromna dysproporcja miedzy prawdopodobieństwami różnych wyników. Dlatego będziemy szukać przybliżenia nie dla P(k), lecz dla \ln P(k).

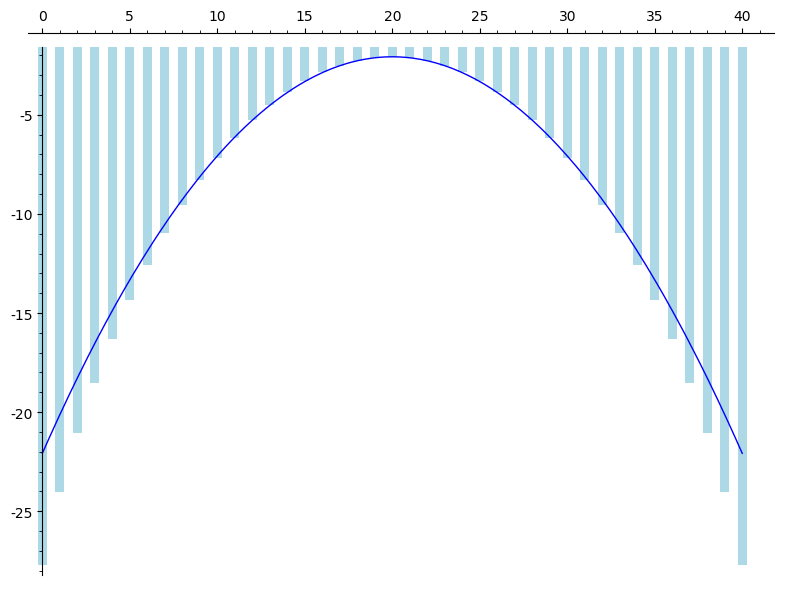
Wykres przedstawia histogram \ln P(k), a także przybliżającą go parabolę. Każdą przyzwoitą funkcję możemy przybliżyć rozwinięciem Taylora:

f(k)=f(k_0)+(k-k_0)f'(k_0)+\dfrac{1}{2!}(k-k_0)^2 f''(k_0)+\ldots.

W maksimum znika pierwsza pochodna, mamy więc

f(k)=f(k_0)+\dfrac{ (k-k_0)^2 f''(k_0)}{2}+\ldots.

Naszą funkcją jest

f(k)=\ln P(k)=\ln n!-\ln k!-\ln (n-k)! +k \ln p+(n-k) \ln q.

Potrzebujemy pochodnej z silni dla dużych wartości k oraz (n-k). Pochodna to przyrost funkcji odpowiadający jednostkowemu przyrostowi argumentu. Ponieważ

\ln k!=\ln 1+\ln 2+\ldots \ln k,

powinna ona być równa

\dfrac{d\ln k!}{dk}=\ln k.

Poniżej uzasadnimy to precyzyjnie, choć ostatni wzór powinien być zrozumiały intuicyjnie: nachylenie funkcji logarytmicznej stopniowo maleje, więc sumę można coraz lepiej przybliżać za pomocą pola pod krzywą.

Odpowiada to przybliżeniu

\ln k! \approx \displaystyle \int_{1}^{k} \ln t \, dt \Rightarrow \dfrac{d\ln k!}{dk}=\ln k.

Warunek na maksimum funkcji przybiera postać

\dfrac{d\ln P(k)}{dk}=-\ln k+\ln (n-k)+\ln p -\ln q =0 \Rightarrow k_0=np.

Druga pochodna równa jest

\dfrac{d^2 \ln P(k)}{dk^2}=-\dfrac{1}{k}-\dfrac{1}{n-k}=-\dfrac{1}{npq}.

Ostatnia równość daje wartość pochodnej w punkcie k=np. Nasze przybliżenie przybiera więc postać

P(k)=P(0) \exp\left(-\dfrac{(k-np)^2}{2npq}\right)+\ldots.

Jest to rozkład Gaussa o wartości średniej np oraz szerokości (odchyleniu standardowym) npq. Wartość P(0) można wyznaczyć z warunku normalizacji: pole pod naszą krzywą powinno być równe 1. Można ściśle pokazać, że przy dużych wartościach n wyrazy wyższych rzędów są do pominięcia przy obliczaniu prawdopodobieństw: różnice między parabolą a histogramem na wykresie dotyczą sytuacji, gdy prawdopodobieństwa są bardzo małe.

Przyjrzymy się teraz bliżej obliczaniu silni z dużych liczb. Zacznijmy od następującej funkcji zdefiniowanej jako całka:

g(t):=\displaystyle \int_{0}^{\infty}\exp(-\alpha t)\, dt,\alpha>0.

Różniczkując ją kolejno n razy po \alpha i kładąc na koniec \alpha=1, otrzymamy

n!=\displaystyle \int_{0}^{\infty} t^{n}\exp(- t)\, dx\equiv \Gamma (t+1).

Otrzymaliśmy funkcję gamma Eulera, która jest uogólnieniem silni, ponieważ zdefiniowana jest nie tylko dla wartości całkowitych n, lecz może być uogólniona na płaszczyznę zespoloną i określona wszędzie oprócz argumentów całkowitych ujemnych. Nam wystarczą tutaj wartości rzeczywiste dodatnie, szukamy przybliżenia dla dużych n. Zapiszmy funkcję podcałkową w postaci wykładniczej i zastosujmy rozwinięcie Taylora wokół maksimum, dokładnie tak jak powyżej dla funkcji P(k):

n!=\displaystyle \int_{0}^{\infty} \exp(n\ln t- t)\, dx\approx \exp(n\ln n-n)\int_{0}^{\infty} \exp\left(-\frac{(t-n)^2}{2n}\right) dt.

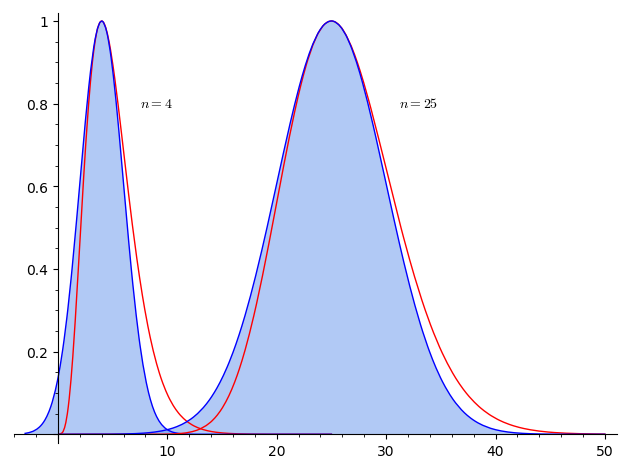
Wykres przedstawia przybliżenie gaussowskie oraz (na czerwono) wartości funkcji po wyłączeniu czynnika \exp (n\ln n-n). W przybliżeniu gaussowskim możemy rozszerzyć dolną granicę całkowania do -\infty, co nawet zmniejsza błąd przy niedużych wartościach n, a niczego nie psuje przy dużych wartościach n. Jeśli przeskalujemy funkcję gaussowską tak, aby miała jednostkową szerokość, porównanie wypadnie jeszcze lepiej.

 

Widzimy więc, że można ostatnią całkę wziąć po całej prostej. Jej wartość jest równa \sqrt{2\pi n}. Otrzymujemy wzór Stirlinga:

\ln n!\approx n\ln-n +\ln\sqrt{2\pi n}+O(1/12n).

Zaznaczyliśmy też wielkość następnego wyrazu w szeregu malejących potęg n. W wielu zastosowaniach można pominąć zupełnie całkę gaussowską i wnoszony przez nią wyraz \sqrt{2\pi n}. Jak się trochę popracuje nad dalszymi wyrazami rozwinięcia Taylora, można otrzymać i tę poprawkę 1/12n.

Pierre Simon Laplace rozwinął techniki szacowania wartości asymptotycznych całek. Jego wyprowadzenie wzoru Stirlinga było elegantsze, lecz rachunkowo trudniejsze (wymagało odwrócenia rozwinięcia w szereg). Laplace wykazał także, iż sumy zmiennych losowych zachowują się jak zmienne gaussowskie także w ogólniejszych sytuacjach niż ta przez nas rozpatrywana. Innymi słowy pierwszy zauważył, że zachodzi tzw. centralne twierdzenie graniczne. Ścisły dowód pojawił się znacznie później.

Dodaj komentarz